티스토리 뷰
라그랑주 승수법?
- 라그랑주 승수법은 제약이 있는 최적화 문제를 푸는 방법으로,최적화하려 하는 값에 형식적인 라그랑주 승수 항을 더하여, 제약된 문제를 제약이 없는 문제로 바꾸는 방법
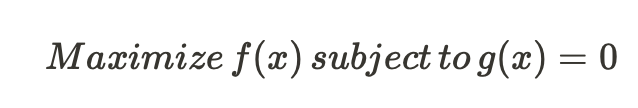
- g(x) = 0이라는 제약식에서 f(x)를 최대화하는 문제를 풀어야 할 때, 라그랑주 승수 −λ 를 g(x) 에 곱해서 f 에 더한 라그랑주 함수 L(x,λ):=f(x)−λg(x) 를 목적 함수로 삼는 다음의 최적화 문제로 바꾸는 방법

- 엄청난 내용은 아니고, 그냥 이론적 증명이나 수식 전개할 때 사용되는 Tricky한 하나의 방법론이라고 이해하면 될 듯!
- 당장 와닿지는 않을 수도 있지만, 논문을 이해한다거나 머신러닝, 딥러닝 모델들의 방법론을 이해할 때 많이 등장하므로 알아두면 도움이 될 것!
라그라주 승수 정리의 기하학적 이해
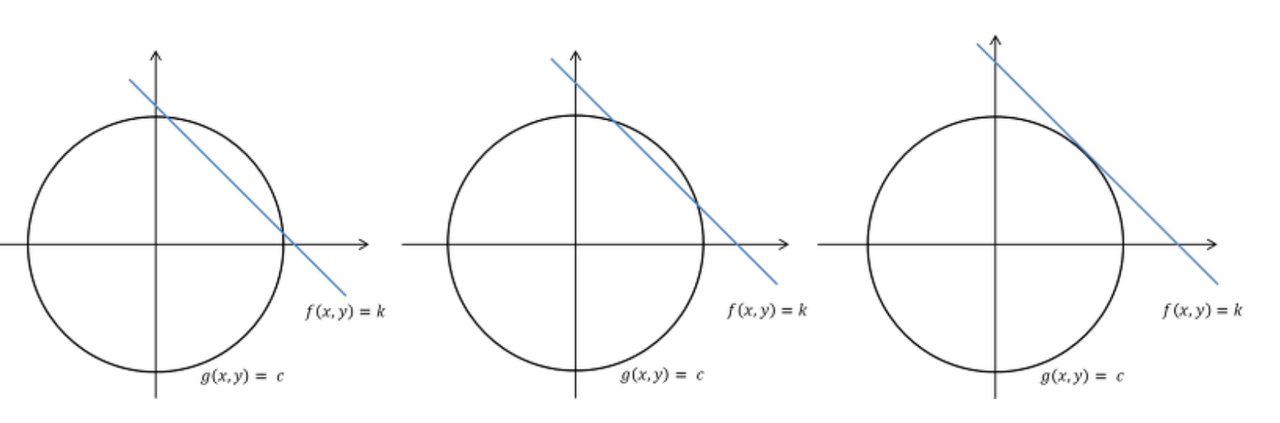
제약 조건 g(x,y)=c를 만족하는 f(x,y)의 최댓값 문제에 대한 기하학적 표현
- 원과 직선이 접할 때, f(x,y)가 최대라는 것을 직관적으로 생각할 수 있음!
- 원과 곡선의 공통 접선의 접점을 찾는 과정이 라그랑주 승수법임
- 이 방법의 발상은 두 함수의 공통 접선에 수직인 벡터 , 즉 두 함수의 기울기 벡터의 방향이 같으면 된다는 것
- 따라서, 두 식을 만족하는 (x,y)를 연립방정식으로 찾아주면 되는데 이때, 기울기 벡터가 서로 상수배인 관계이므로 임의의 상수인 λ 를 곱해서 연립방정식을 풀어주면, 두 함수의 접점을 찾을 수 있음!
- 라그랑주 승수법은 단순히 f라는 함수의 최댓값 or 최솟값을 찾아주는 것이라기 보다는 g(x,y) = 0이라는 제약 조건 하에서 최댓값이나 최솟값을 찾는 방법임!
Scipy 를 사용하여 등식 제한조건이 있는 최적화 문제 계산하기
사이파이의 optimize 서브패키지는 제한조건이 있는 최적화 문제를 푸는 fmin_slsqp() 명령을 제공
fmin_slsqp(func_objective, x0, eqcons=[func_constraint1, func_constraint2])
- fmin_slsqp() 명령은 목적함수와 초깃값, 그리고 제한조건 함수의 리스트를 인수로 받음
- 목적함수는 배열인 인수를 받도록 구현되어야 하고 제한조건 함수의 경우에는 항상 eqcons 인수를 명시해야 함!
import scipy as sp
import numpy as np
def f1array(x):
return x[0] ** 2 + x[1] ** 2
def eq_constraint(x):
return x[0] + x[1] - 1
sp.optimize.fmin_slsqp(f1array, np.array([1, 1]), eqcons=[eq_constraint])
라그랑주 승수법 in ML / DL
- 확률론 MLE 찾기
- PCA
- SVM (서포트 벡터 머신)
MLE
카테고리분포의 최대가능도 모수 추정
- d개의 카테고리를 갖는 카테고리 분포, 𝑥 는 모두 𝑘개의 원소를 가지는 원핫인코딩(one-hot-encoding)벡터

PCA
- 데이터의 분산을 최대한 보존하면서, 서로 다른 직교하는 축을 찾아서 고차원을 저차원으로 선형 변환하는 기법
- 변수가 너무 많을 경우 모델이 데이터에 과적합 될 수 있음. -> 차원축소의 필요성
- 예를 들어, 10개의 변수가 있는데 정보의 손실 없이 이를 2개의 변수로 차원축소해주고 싶으면, 이때 PCA를 활용!
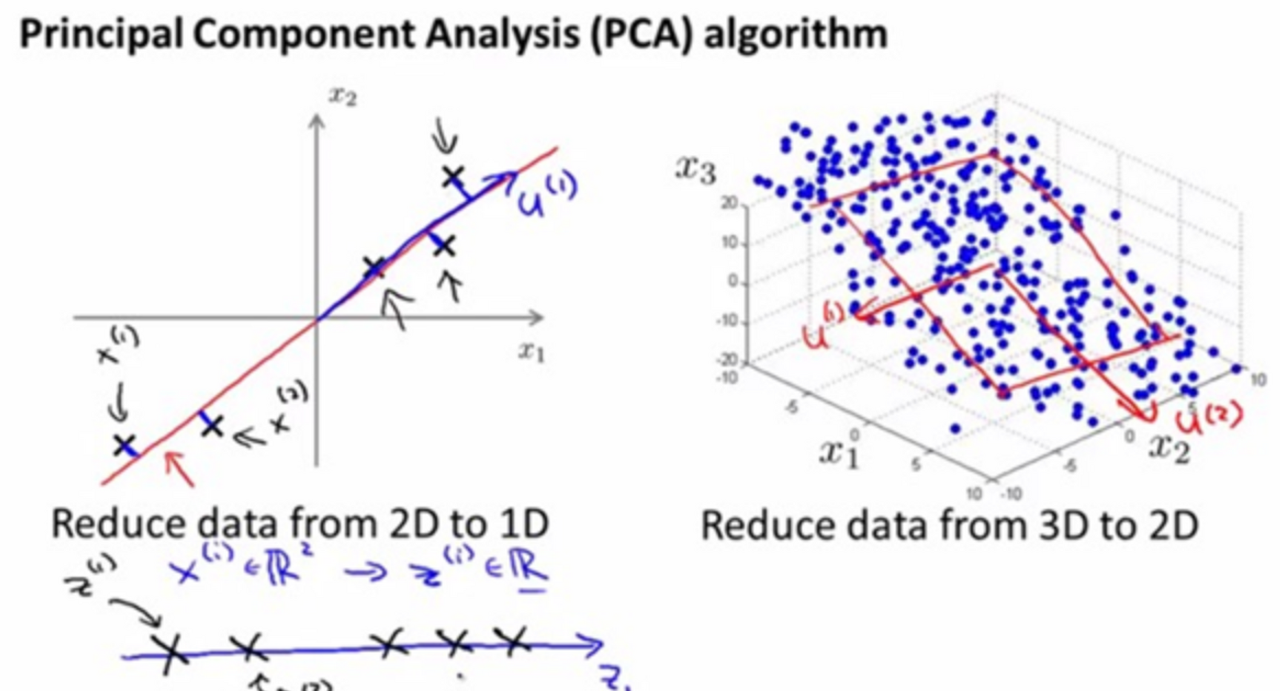
- PCA를 저차원으로 투영된 데이터의 분산을 최대화하는 최적화 문제로 정의할 수 있음
- 하지만, 이때 벡터 u의 크기에 비례하여 분산의 크기도 커질 수 있으므로, 라그랑주함수를 추가하여 벡터 u를 단위벡터로 크기를 제한

SVM
[참고 자료]
- [베이지안 딥러닝] Lagrange multipler and KKT multiplier
- https://www.youtube.com/watch?v=lmD9p6J_-TA
- https://datascienceschool.net/02
- https://freshrimpsushi.github.io/posts/lagrangian-multiplier-in-optimization-theory
- https://untitledtblog.tistory.com/96
- https://datascienceschool.net/02 mathematics/05.02 제한조건이 있는 최적화 문제.html
'AI | DS' 카테고리의 다른 글
| LLM 활용 Reranking 방법론(Utilizing LLMs as Unsupervised Rerankers) (0) | 2024.07.09 |
|---|---|
| RAPTOR: RECURSIVE ABSTRACTIVE PROCESSING FOR TREE-ORGANIZED RETRIEVAL 논문 리뷰 (0) | 2024.05.29 |
| Langchain 정리 (2) | 2024.03.17 |
| Transformer 톺아보기 (1) Positional Encoding (2) | 2023.11.26 |
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- ORDER BY LIMIT
- 서브쿼리
- cold-start
- WHERE문 집계함수
- SELECT문 안 서브쿼리
- 하이브리드 필터링
- 이코테
- 추천시스템
- reranker 속도 개선
- Lagrange Multipler
- 연관규칙분석
- 알고리즘
- NULL인 열 만들어주기
- pointwise reranker
- llm reranker
- 하나의 테이블에 대한 조작
- 여러개 값에 대한 조작
- SQL레시피
- SASRec
- groupby 다중
- reranker
- SET문
- rag 다중문서 활용
- SQL
- WHERE절서브쿼리
- treer구조
- 다중 GROUP BY
- 고전적 추천 알고리즘
- NULL AS
- 숨겨진조건
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
글 보관함
